π>3.05を証明せよ ―― 東大の伝説の入試問題をプログラムで解く:組み込みエンジニアの現場力養成ドリル(27)(5/5 ページ)
面積から円周率を求める別解法?
面積から円周率が求められるなら、図3を図10のように、三角形を移動すればスタイリッシュに解けるのではと考えました。三角形Eを図10のように移動させると、凹四角形Dの面積が1*3で3になることが視覚的にも分かります。三角形BとEが4×3の長方形、三角形AとFをくっつけると3×1の長方形になり、これに三角形Cを足せば、非常に簡単に円の内側の面積を求められますね。
面積=4*3+3*1+3*1+1*1*1/2=18+1/2
円周率=(18+1/2)*4/(5*5)=2.96
円周率が2.96になり、3.05どころか3にも届きません。半径10の円の面積から計算した円周率が2.61だったことを考えると、面積から円周率を計算する方法は、外周を計算するより、効率が悪く、収束が遅いようです。東大の伝説の難問は簡単ではありません。
モンテカルロ法は使えないか?
「プログラミングで円周率を計算する」と聞いて、乱数を発生させるモンテカルロ法を思いついた方もいるでしょう。モンテカルロ法は、例えば、図11のように、x軸の座標とy軸の座標のペアを0から10までの乱数を大量に発生させて作り、正方形全体に落ちた点の数と、円の内部に落ちた点の数の比率から、円周率を求めるものです。
モンテカルロ法は、全くデタラメな数値から、円周率のような「キチンとした値」が求められる面白い手法ですが、今回の課題では使えません。モンテカルロ法では、使う乱数が「正しくデタラメ」であることを統計的に検証する必要があります。これは非常に大変ですし、確率的にしか求められないので、入試問題の解法としては適切とは思えません。わざわざ複雑な乱数を使う必要はなく、素直に規則正しく面積を求める方が簡単で、説得力があります。
逆に、大量に発生させた乱数から求めた円周率が、3.1415……に近づけば、「正しくデタラメな乱数」であることが分かるかもです。
プログラミングを数学の証明に使えるか?
解析的ではなく、数値的に離散数学的に課題を解くのがプログラミングです。コンピュータは数学の証明に使えないのではないか? そう思った方は多いでしょう。
例えば、図6の方法で円周率を計算することは、「面積を点の数とし、ピタゴラスの定理により、点が円内か円外かを整数の掛け算で判断する」、また、「大量の計算をコンピュータが肩代わりしている」ので、加減乗除しかできない電卓を1000人が持ち、計算の手助けをしてもらっているのと同じです。巨大な数が素数かどうかをスーパー・コンピュータで延々と割り算を繰り返すのと同じで、「コンピュータを使ったから、素数かどうかは証明できない」とは言えません。ただし、プログラムの中にバグがないと仮定しています。
コンピュータを使って、力まかせに数学の問題を証明したのが、有名な「4色問題」です。「2次元の地図であれば、どんなに入り組んでいても、4色あれば、隣接する領域を異なる色で塗り分けられる」ですね。ただし、米国にある「フォー・コーナーズ(図13参照)」のように、1点のみで接する場合は、「隣接している」とはみなしません。
1976年、イリノイ大学アーバナシャンペーン校のケネス・アッペルとヴォルフガング・ハーケンが、地図を約2000のパターンに分類し、それをコンピュータで演算して「地図は4色で塗り分けられる」ことを証明しました。証明は、一応、認められ、記念切手も発行されたのですが、演算量が多すぎて人間の手では処理が正しいことを検証できないことや、プログラムにバグがあるかもしれないため、「完全には証明されていない」と考えた数学者もいました。
その後、プログラムをデバッグしたり、アルゴリズムを改良したり、別の研究者も同じ結果になったことから、現在では「証明された」とみなしています。
通常、山脈の稜線、河、湖が国境や州境になりますが、この4州には州境になりそうな目立った自然物がなく、経線と緯線に沿って東西南北に90度で直角に切りました。4州が接する「フォー・コーナーズ」には、モニュメントが埋め込んであります。この州境は、人工的な境界線であり、JR中央線が、東中野駅〜立川駅の24.7kmが一直線になった理由と似ています。
おわりに
今回は、大学の入試問題をソフトウェア的に解きました。視点を変えると、意外な解法が見えますね。入試問題や数学の証明で使う場合でも、プログラムの品質は非常に重要です。
コロナウイルス禍により、自宅でプログラムを開発しているエンジニアの方々は多いでしょう。気分転換のつもりで、いろいろな大学入試問題をプログラムで解いてみてはどうでしょう? C言語の開発環境は、例えば、こちらのサイト(http://9cguide.appspot.com/p_9cide.html)から無料でダウンロードできます。
/* 半径が 100 でパイを計算する */
#include <stdio.h>
int main(void){
printf("パイの計算(半径は100)\n");
int x, y;
float area, pi;
area = 0;
pi = 0;
/* (0.0)から(100,100)まで、ピタゴラスの定理により、「Xの2乗 + Yの2乗」を計算。 */
for (x = 0; x <= 100; x++) {
for (y = 0; y <= 100; y++) {
if (x*x + y*y <= 10000) {
/* 「Xの2乗 + Yの2乗」 ≦ 10,000 なら円の中なので「円内の点の数」に1を加算。*/
/* → 図6の「黒い点」の数をカウントする。 */
area = area + 1;
}
}
}
/* 「4分の1の円の点の数」から、x = 0 の点の数を減算する(101を減じる)。*/
/* → 図6の「緑の点」の数を減じる。 */
area = area - 101;
printf("4分の1の点の数 = ");
printf("%.0f\n", area);
/* 「4分の1の点の数」を4倍し、(0,0)の引き過ぎ分の1を加算し、全体の点の数を算出*/
area = area * 4 + 1;
printf("全体の点の数 = ");
printf("%.0f\n", area);
/* 点の数(面積)を 半径の点の数(101)の2乗で除算すると、パイを計算できる。*/
pi = area / (101*101);
printf("pi = %.5f", pi);
}
関連記事
 全数検査の落とし穴 ―― 全人口にPCR検査をしても意味がない数学的な理由
全数検査の落とし穴 ―― 全人口にPCR検査をしても意味がない数学的な理由
新型コロナウイルスの感染拡大が続く中で、もっと広く、多くの人へのPCR検査実施を求める声があります。ただ、私は「日本の全人口に対しPCR検査をしても、感染状況の実態は全く把握できない」と数学的に思っています。その理由を見ていきましょう。 スマホで極秘通信するには? 米高官が使った「簡単なのにバレない」情報の送受信法
スマホで極秘通信するには? 米高官が使った「簡単なのにバレない」情報の送受信法
今回は、8年前、アメリカで実際に起きた有名なスキャンダルを題材に、スマートフォンで極秘に通信する“簡単な方法”を考えてもらいます。 集合論のパラドックス:命題が正しいのに対偶が正しくない!? 〜私語をした学生への罰レポートより
集合論のパラドックス:命題が正しいのに対偶が正しくない!? 〜私語をした学生への罰レポートより
今回は、私語をした学生に筆者が「罰レポート」として課した“集合論の難解な問題”を取り上げます。 「赤か? それとも青か?」――機能共有の悲劇がもたらした混乱するトイレのUI
「赤か? それとも青か?」――機能共有の悲劇がもたらした混乱するトイレのUI
なぜこのようなユーザーインタフェースが存在するのか……。日ごろの生活の中で筆者が見つけた“良くないユーザーインタフェース”から学びを得る。「京急蒲田駅」「JR渋谷駅」に続き、筆者を悩ますのはトイレの蛇口。今回はその問題点を紹介すると同時に、解決策を検討する。 東京の地下鉄「三田線」をアルファベット1文字でどう表す? ―― 都道府県名を1文字にコード化せよ(その1)
東京の地下鉄「三田線」をアルファベット1文字でどう表す? ―― 都道府県名を1文字にコード化せよ(その1)
米国の州の名前を2文字で表したり、東京の地下鉄の路線名を1文字のアルファベットで略したりする場合、関係者はとても苦労したはずです。そんな苦労を読者自身に体験していただき、最終的なテーマである「都道府県名の1文字化」を考えます。「その1」の今回は、米国の州名略称と、東京の地下鉄路線名の略称/コード化を取り上げます。 パニック間違いなし!? 難易度高めな迷宮「京急蒲田駅」がUI的に絶対NGな理由
パニック間違いなし!? 難易度高めな迷宮「京急蒲田駅」がUI的に絶対NGな理由
日常生活のありとあらゆるモノから、ユーザーインタフェース(UI)の“良しあし”を学ぶことができます。日ごろ学生たちにユーザーインタフェースに興味を持つよう指導する筆者が「これは絶対にアカンやろ」と思わず叫んでしまったのが「京急蒲田駅」です。ユーザーインタフェースの観点だけでなく、機能構造の意味でも“絶対NG”な京急蒲田駅から学べることとは何か、一緒に考えてみましょう。
Copyright © ITmedia, Inc. All Rights Reserved.
会員登録がまだの方はこちら
豊富なホワイトペーパーの中から、製品・サービス導入の検討に役立つ技術情報や導入事例などを簡単に入手できます。
特集
- 設計者CAEの取り組みに関する実態
- マテリアルズ・インフォマティクスの動向調査
- 製造業のアナログ業務の実態調査
- 設計・解析業務におけるAI活用
- 製造現場におけるデータ活用の実態調査
- 3Dプリンタ利用動向調査
- CAD利用動向調査
- 研究・開発職のデジタル活用調査
- 安全安心なIoT機器実現の課題
- 電気設計者の課題と解決
- “つながる工場”の現状と課題
- 製造業におけるAI開発および活用の実態
- 設計・製造現場における品質管理
- 製造業IoTセキュリティ
- IoT時代の組み込みソフトウェア品質
- IoT時代のセキュリティリスクに備える
- 加速する工場と生産設備のデジタル化
- 製造業の省エネ対策と課題
- モノづくり設計者のワークスタイル調査
- タイアップ&セミナーコンテンツ一覧

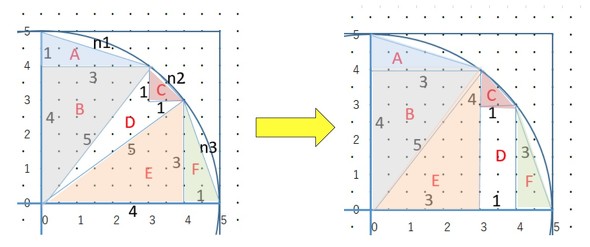
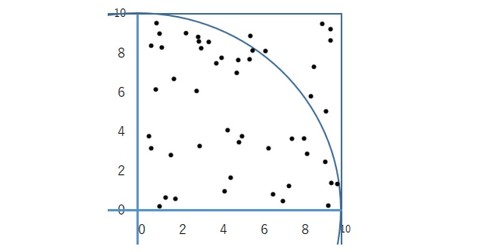 図11:モンテカルロ法による円周率の計算
図11:モンテカルロ法による円周率の計算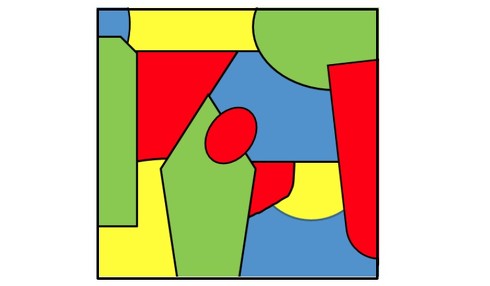 図12:コンピュータを使って証明した4色問題
図12:コンピュータを使って証明した4色問題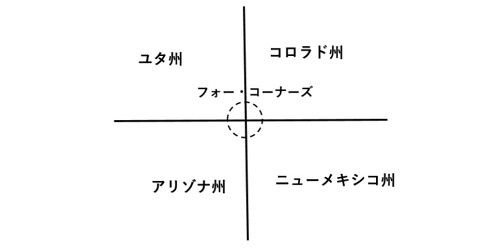 図13:4つの州が1点で接する「フォー・コーナーズ」
図13:4つの州が1点で接する「フォー・コーナーズ」



