π>3.05を証明せよ ―― 東大の伝説の入試問題をプログラムで解く:組み込みエンジニアの現場力養成ドリル(27)(3/5 ページ)
円周率とは?
授業で学生に、「πってなんだ?」と聞くと、「円周率です」と答えるので、さらに、「じゃあ、円周率ってなんだ?」と聞くと、「3.14です」と答える場合が少なくありません。そんな場合、さらに踏み込んで、「じゃあ、なぜ、3.14なんだ?」と迫ると、「えっ、アルキメデスの昔からその値です。関数電卓でもその値を表示します」となり、どうも、円周率の意味が分かっていないようです。「円周率を具体的にどうやって計算するんだ? この教室の中にあるものを使って計算してみて」と言うと、頭を抱えて悩む学生が多数……。「除夜の鐘は108」みたいなイメージなのかもしれません。
さらに、「じゃあ、半径がrの円の面積はどうやって求めるんだ?」と聞くと、「r*r*πです」と答えるので、「なぜ、それで円の面積が計算できるんだ?」と畳みかけると、「エッ……」と絶句してしまいます(絶句したいのは私です)。そこで、私は、図1のような円を描いて、説明します。
「いいですか、皆さん、円周率とは、円周Pの長さが、直径Rの何倍かを表したものです。ドラム缶のような円形のものがあれば、糸を巻いて円周を計り、直径も定規で計って、割り算すれば、円周率を求められます。ドラム缶ぐらい大きいと、円周率は3.1ぐらいにはなりますよ。では、円の面積の求め方です。図2を見てください」
円の面積の求め方は、一種の積分の考え方ですね。例えば、図2の左のように、円をピザのように6等分して、それを図2の右のように互い違いに組み合わせます。すると、長方形(正確には平行四辺形)になります。6等分を急激に細かくすると、最終的には、円の面積は、「高さ×横」で、「半径×円の半周」となります。すなわち、(直径の半分)×(直径×円周率×1/2)で、「半径×半径×円周率」になり、「いつもの見慣れた円の面積の公式」になります。
伝説の入試問題
以上が、今回のテーマのイントロダクションです。本編の話より枕(イントロ)が長い柳家小三治の落語みたいですね(私がお金を払って聞きに行った「落語家三銃士」が、立川談志、古今亭志ん朝、柳家小三治で、このうち、存命なのは小三治だけです……)。では、ここで、問題です。
問題2(制限時間30分)
以下の伝説的な東大入試問題を①幾何学的に解いてください。そして、②別の解法でソフトウェア的に(=プログラムをコーディングして)解いてください。それぞれ15分、合計30分で解答してください。
円周率が3.05より大きいことを証明せよ。
Copyright © ITmedia, Inc. All Rights Reserved.
会員登録がまだの方はこちら
豊富なホワイトペーパーの中から、製品・サービス導入の検討に役立つ技術情報や導入事例などを簡単に入手できます。
特集
- 設計者CAEの取り組みに関する実態
- マテリアルズ・インフォマティクスの動向調査
- 製造業のアナログ業務の実態調査
- 設計・解析業務におけるAI活用
- 製造現場におけるデータ活用の実態調査
- 3Dプリンタ利用動向調査
- CAD利用動向調査
- 研究・開発職のデジタル活用調査
- 安全安心なIoT機器実現の課題
- 電気設計者の課題と解決
- “つながる工場”の現状と課題
- 製造業におけるAI開発および活用の実態
- 設計・製造現場における品質管理
- 製造業IoTセキュリティ
- IoT時代の組み込みソフトウェア品質
- IoT時代のセキュリティリスクに備える
- 加速する工場と生産設備のデジタル化
- 製造業の省エネ対策と課題
- モノづくり設計者のワークスタイル調査
- タイアップ&セミナーコンテンツ一覧

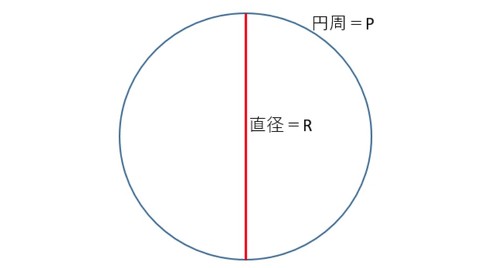 図1:円周率の説明
図1:円周率の説明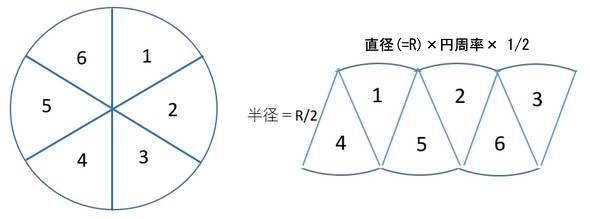 図2:円の面積を求める方法
図2:円の面積を求める方法



