ソフトウェア工学的には羽生善治の「5二銀」は最善手ではない!? 東工大入試問題をプログラムで解く：組み込みエンジニアの現場力養成ドリル（32）（1/4 ページ）

[山浦恒央 東海大学 大学院 組込み技術研究科 非常勤講師（工学博士），TechFactory]

　第27回目の本コラムでは、東大の伝説の入試問題、「π＞3.05を証明せよ」を取り上げました。大学の入試問題として、おそらく世界で最少文字数でしょう。この問題は、余弦定理を応用して解くのが受験での王道ですが、同コラムでは、ピタゴラスの定理だけで解く方法と、C言語によるプログラミングで証明する2つの解法を示しました。ピタゴラスの定理だけでも解けるので、中学3年生でも正解できます。

　今回は、東工大の2012年度入試問題（数学）を取り上げます。これをプログラミングで解いていただきますが、今回のテーマは単に「難解な入試問題をC言語で解く」という「10分間ミステリーのような意外性を楽しむ頭脳ゲーム」ではありません。その一歩先の「誰にでも簡単に理解できるアルゴリズムとはどういうものか」という「ソフトウェア開発の永遠の課題」を考えることにあります。

日本人は奇襲攻撃が大好き

　昔から、日本の軍人には、「中大兄皇子と中臣鎌足の大化の改新」「織田信長の桶狭間の戦い」「東郷平八郎の対馬沖海戦」「日本海軍による真珠湾攻撃」の4つが頭の中にこびりついています。「自軍には相手の20％の軍勢しかいない、あるいは、貧弱な装備しかないけれど、頭脳的な作戦で巨大な敵を倒す」ことが素晴らしいと評価する傾向にあります。防御が最も厚い正面から突破するのではなく、相手の油断や虚をつき、手薄な横から奇襲攻撃することがカッコいいとの考え方は、現代の日本の会社のビジネス戦略、個人の日常生活の行動、囲碁将棋までしっかり染みついています。

　一方、米国の軍事戦略の基本は「物量作戦」です。圧倒的な軍事力、資源に物を言わせ、時間をかけて、正面からじりじりじわじわと相手を寄り切ることが王道と考えています。日本の自衛隊は、定期的に米国本土での合同軍事演習を実施しており、訓練の中には日米に分かれての模擬戦闘があります。米軍の幹部から「自衛隊側は、不利な状況で奇襲攻撃をかけてくることが多く、自殺的行為に思える」とのコメントと聞いたことがあり、お互いの基本戦略の違いが明確に出ていると感じました。

将棋の伝説の妙手

　囲碁や将棋には歴史的妙手があります。囲碁では、本因坊秀策の耳赤の手、坂田栄男の逆ノゾキ、加藤正夫のツケ、将棋では升田幸三の3五銀、羽生善治の5二銀、藤井聡太の7七飛成が有名です。

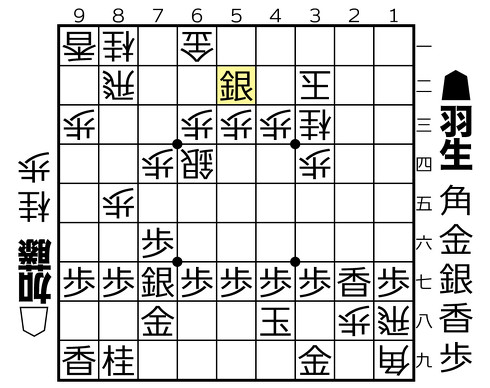
　私が今でも強烈に覚えているのが、第38回NHK杯テレビ将棋トーナメントの4回戦、羽生善治五段対加藤一二三九段戦（段位は当時）で、羽生五段が敵陣にタダで打ち込んだ61手目の5二銀です（図1参照）。

　対局は1989年1月9日、元号が平成に変わった翌日で、テレビ放映が2月5日の日曜日でした。テレビ解説の米長邦雄九段が5二銀を見た瞬間、「おぉー」と奇声を発したことで印象に強く残っています。後には、相手の加藤九段がこの手を見て座布団から30cmも飛んだとの尾ひれも付きました。

　タダ捨てに打った5二銀を後手が何で取っても、2七の香車が2筋に効いているので、先手の1四角で即詰みになります（△5二同金ないし△5二同飛でも、▲1四角、△4二玉、▲4一金で詰み）

図1：歴史的妙手、羽生五段の5二銀（NHK杯第38回将棋トーナメント4回戦第1局61手目）

　羽生五段の5二銀のような妙手は、意外性が満載で派手だしカッコいいので、しっかり記憶に残りますが、プロやアマを問わず、囲碁や将棋でこんな「妙手一閃」で勝負が決まることは非常にまれ。ほとんどは、囲碁の場合、厚みや地で少しずつ相手を上回り、将棋の場合、駒得を徐々に重ねて優勢を拡大して勝利する場合がほとんどです。実戦では、妙手を放つより、正面から攻めジワジワと手得を重ねて差を広げ、最後は物量で圧倒する勝ち方が多いと思います。

　ソフトウェア開発でも同じで、妙手のようなカッコいい処理方式より、正面から泥臭くぶつかり、単純な物量作戦で処理する方が優る場合が少なくありません。

東工大2012年度入試を解く

　以下の東工大の2012年度入試問題を例に、物量作戦の良さを体感していただきます。まずは、この問題をプログラミングで解いてください。

問題1（制限時間15分）

　10000以下の自然数 n において、[√n] が n の約数となるものの個数を求めよ。

　ただし、[ ] は、ガウス記号で、小数点以下を切り捨てた値である（東工大2012年度）。